FAQ

It’s about the computation of the first occurrence of gaps between consecutive prime numbers and is part of a wider effort researching aspects of Goldbach’s conjecture, one of the oldest and best-known unsolved problems in number theory - and all of mathematics.

Goldbach’s conjecture in modern form is “every even number larger than four is the sum of two odd prime numbers”. The conjecture has been shown to hold for all integers less than $4\; ·\; 1018$ but remains unproven despite considerable effort.

The computation of the first occurrence of prime gaps of a given (even) size between consecutive primes has some theoretical interest. Richard Guy (Erdős number 1) assigns this as problem A8 (“A8 Gaps between primes. Twin primes”) in chapter 1 (“Prime Numbers”) of his book “Unsolved Problems in Number Theory”. Guy’s description of A8 is usefully available to read online at Google books (scroll down to p31).

To describe the problem precisely we need to establish some terms, so ... if we let p_k be the k^th prime number, i.e. $p$₁=2, $p$₂=3, $p$₃=5, ..., and let $g$_k=p_(k+1)-p_k be the gap between the consecutive primes $p$_k and p_(k+1). The interest is in how $g$_k (the size of the gap) grows as the size of the prime numbers grows.

In 1936, in a paper submitted to Acta Arithmetica titled “On the order of magnitude of the difference between consecutive prime numbers”, Swedish mathematician Harald Cramér offered a conjecture --- based on probabilistic ideas --- that the large values of $g$_k grow like $(log\; p$_k)^2.

The actual problem is that our empirical data does not allow us to discriminate between the growth rate conjectured by Cramér and other conjectured possible growth rates, say $(log\; pi(p$_k))^2 for example (where $pi(x)$ is the usual prime counting function and $pi(p$_k)=k.)

Another example is identified by Tomás Oliveira e Silva in Gaps between consecutive primes where he observes that his empirical data suggests yet another growth rate, namely that of the square of the Lambert W function --- or “omega function” (not the title of a Robert Ludlum thriller, I learn).

The trouble is that these growth rates differ by very slowly growing factors (such as $log\; log\; p$_k) and much more data is needed to verify empirically which one is closer to the true growth rate.

The actual actual problem is that right now, we don’t know of any general method more sophisticated than an exhaustive search for the determination of first occurrences and maximal prime gaps.

In essence, we’re limited to sieving successive blocks of positive integers for primes, recording the successive differences, and thus determining directly the first occurrences and maximal gaps. And, as the size of the prime numbers increases, so does the amount of computational effort required to do the sieving, etc.

Large (or small) gaps can be more interesting if they are of sufficient merit. A gap’s merit indicates how much larger the gap is than the average gap between primes near that point (the average being $ln(x)$ as a consequence of the Prime Number Theorem). The greater the merit, the more unusual the gap. The more unusual the gap, the more interesting it is, as an outlier, from a number theory perspective.

The following graph (taken from Tomás Oliveira e Silva’s Gaps between consecutive primes) charts the available values of $P(g)$ that they were able to compute (between 2001 and 2012) and illustrates the principle of merit. The black line represents the lower bound for $P(g)$ suggested by Cramér's conjecture, the white dots are gaps between probable primes.

The noticeable outlier - the gap of 1132 - is of significance to the related conjectures put forth by Cramér (1936) and Shanks (1964), concerning the ratio $g/ln2(p$₁). Shanks reasoned that its limit, taken over all first occurrences, should be 1; Cramér argued that the limit superior, taken over all prime gaps, should be 1. Granville (1994), however, provides evidence that the limit superior is $>=\; 2exp(-gamma)=\; 1.1229$. For the 1132 gap, the ratio is 0.9206, the largest value observed for any $p$₁ > 7 thus far.

Over the last few decades, exhaustive search has continued to push the envelope, courtesy of faster computers and concerted effort.

All prime gaps in have now been analyzed, where $264=\; 18446744073709551616$, the smallest positive integer requiring more than 64 bits in its binary representation i.e. not representable in C as a uint64_t. The final push from 18446744000000000000 to $264$ was carried out by the combined efforts of members of the Prime Gap Searches (PGS) project at the Mersenne Forum: Jerry LaGrou, Dana Jacobsen, Robert Smith, and Robert Gerbicz.

Primality tests take longer, so the whole search process takes longer. For example, searches with 11k digit numbers are very slow.

Empirically in the 100-8000 digit range, the BPSW test is about $O(log2.5(n))$, i.e. 2x larger size is 5-6x longer time.

The larger size also means a longer range for a large merit, which means more tests. Presumably $log(n)$ growth. There is a complicating factor of the partial sieve that has a dynamic $log2(n)$ depth.

Usually the tradeoff is that small sizes run faster but are better covered, hence need high merits to get a record. Large sizes (200k+) are slow but are so sparse that almost anything found is a record.

The sweet spot this year (2015 at the time of writing) seems to be in the 70-90k range for efficiency of generating records. There are lots of gaps with merit under 10.

A little experiment looking at the time and number of merits >= 5.0 found using $k\ast p\#/30-b$ where k=1..10000 without multiples of 2,3,5.

p=20:  1.7s  102 found = 60/s (28-30 digits)
p=40:  4.1s  236 found = 58/s (69-71 digits)
p=80:  19.6s 515 found = 26/s (166-169 digits)
p=160: 235s  985 found =  4/s (392-395 digits)

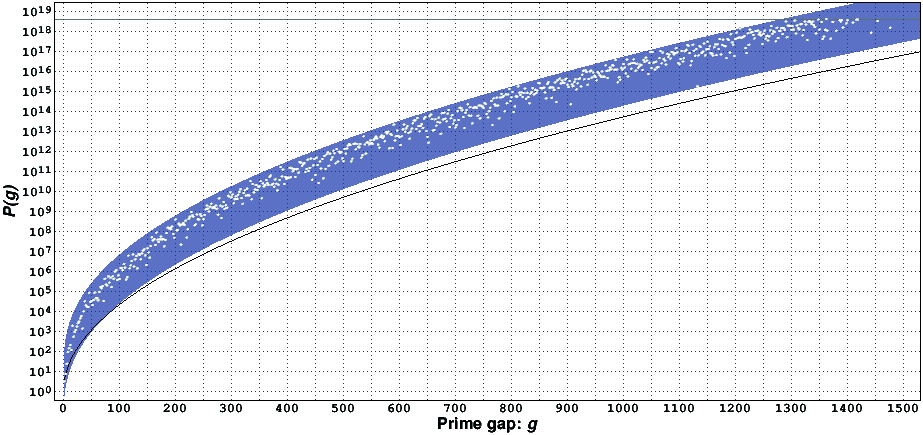
Interestingly with this form, the number we find with merit >= 5 goes up as p gets larger but the time taken goes up quite a bit faster. This explains the shape of the graph of current records: high at the beginning and dropping off as gap size increases.

It’s certainly possible that a different method of selecting the search points would be more efficient and it’s also possible to improve the speed of this or other methods vs. doing prev/next prime with my GMP code.

For example with numbers larger than ~3000 digits using gwnum would be faster than GMP. Gapcoin uses a different method but it’s not obvious how to get exact efficiency comparisons.

Answered by Dana Jacobsen, edited.

There is little point in looking for gaps <1,352 as an exhaustive search of primes up to 4 · 10¹⁸ has been carried out and all gaps smaller than this have been found.

As of the summer of 2014, the Nicely site had early instance prime gaps with merit > 10 listed for all possible gaps < 60,000 and an early effort by the Mersenne Forum has been to extend the early instance list up to 100,000.

At the far end of the scale, the Mersenne Forum is helping to support the largest gap search, looking at a candidate gap (4,680,156) provide by Mersenne Forum member mart_r. This has a merit > 20.

The following two are only 100% accurate within the range given.

• For 64-bit inputs, BPSW. There are also other known methods, and the optimal solution is a mix. The result is unconditionally correct for all 64-bit inputs, and is extremely fast. It’s also commonly used on larger inputs as a compositeness test (sometimes called a probabilistic primality test), as it is fast and has no known counterexamples, with some good underlying reasons as to why we expect them to be rare.
• For up to about 82-bit inputs, deterministic Miller-Rabin. This is a fairly recent result.

All the following methods (ECPP, APR-CL, and AKS) are unconditionally correct for all sizes if they give an output, and all finish in polynomial time for the input sizes that are at all practical on today’s computers (e.g. finishing withing 100 years on a large cluster).

• For heuristic polynomial time, ECPP using Atkin-Morain methods. It is $O(log5n)$ or $O(log4n)$ depending on implementation. It is not guaranteed to finish in this time, but there well-written heuristic analyses that show this complexity, and many millions of runs of practical software showing it matches those results. Primo uses ECPP. Almost all recent general-form proof records in the last 20 years have been done with ECPP. The output includes a certificate of primality which can be verified in guaranteed polynomial time (with a small exponent).
• APR-CL is another good method that is polynomial time in practice although not asymptotically so (the exponent has a factor of $log(log(log(n)))$ in it, which is less than a small constant for any size $n$ we would be applying it to). Pari/GP uses this. It does not output a certificate.
• AKS is deterministic and polynomial-time for all general form inputs or all sizes. and unconditionally correct like the others. It is also horrendously slow in practice. It is not used in practice because we have much better methods.

If you’re writing a paper or dealing with theoretical complexity, just say “AKS shows this problem is in P” and move on. That is the “best” result considering it’s short and people will nod and move on to the rest of your paper.

For small inputs such as 64-bit (numbers smaller than 18,446,744,073,709,551,616), we’ve known for a few years that BPSW is unconditionally correct. It is extremely fast and easy. Slightly easier to program are best-known deterministic Miller-Rabin base sets. For 32-bit the optimal solution seems to be trial division for tiny inputs and a hashed single-base Miller-Rabin test for the rest.

For use in practice, APR-CL or ECPP. They don’t check every box that AKS does (non-randomized and asymptotically polynomial), but they finish in polynomial time for numbers the size we care about, with a lower exponent and much less overhead than AKS.

If you want a certificate, then ECPP. This lets others quickly verify that the result actually is prime rather than just taking it on trust that you ran the test. APR-CL and AKS do not have certificates.